ANÁLISIS DIMENSIONAL
1.-DEFINICIÓN: Es una herramienta que permite simplificar el estudio de cualquier fenómeno en el que estén involucradas muchas magnitudes físicas en forma de variables independientes. Su resultado fundamental, el teorema de Vaschy-Buckingham (más conocido por teorema  ) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada dimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:
) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada dimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:
 ) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada dimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:
) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada dimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:- Analizar con mayor facilidad el sistema objeto de estudio
- Reducir drásticamente el número de ensayos que debe realizarse para averiguar el comportamiento o respuesta del sistema.
2.-APLICACIONES:
- Detección de errores de cálculo.
- Resolución de problemas cuya solución directa conlleva dificultades matemáticas insalvables.
- Creación y estudio de modelos reducidos.
- Consideraciones sobre la influencia de posibles cambios en los modelos, etc.
| Magnitud Derivada | F.D. | Unidad | Tipo |
| Área o Superficie | L2 | m2 | E |
| Volumen o Capacidad | L3 | m3 | E |
| Velocidad lineal | LT-1 | m/s | V |
| Aceleración lineal | LT-2 | m/s2 | V |
| Aceleración de la Gravedad | LT-2 | m/s2 | V |
| Fuerza, Peso, Tensión, Reacción | MLT-2 | kg . m/s2 = Newton (N) | V |
| Torque o Momento | ML2T-2 | N . m | V |
| Trabajo, Energía, Calor | ML2T-2 | N . m = Joule (J) | E |
| Potencia | ML2T-3 | Joule/s = Watt (W) | E |
| Densidad | ML-3 | kg/m3 | E |
| Peso específico | ML-2T-2 | N/m3 | E |
| Impulso, ímpetu, Impulsión | MLT-1 | N . s | V |
| Cantidad de Movimiento | MLT-1 | kg . m/s | V |
| Presión | ML-1T-2 | N/m2 = Pascal (Pa) | E |
| Periodo | T | s | E |
| Frecuencia Angular | T-1 | s-1 = Hertz (Hz) | E |
| Velocidad Angular | T-1 | rad/s | V |
| Aceleración Angular | T-2 | rad/s2 | V |
| Caudal o Gasto | L3T-1 | m3/s | E |
| Calor Latente específico | L2T-2 | cal/g | E |
| Capacidad Calorífica | ML2T-2q-1 | cal/°K | E |
| Calor Específico | L2T-2q-1 | cal/g.°K | E |
| Carga Eléctrica | IT | A . s = Coulomb (C) | E |
| Potencial Eléctrico | ML2T-3I-1 | J/C = Voltio (V) | E |
| Resistencia Eléctrica | ML2T-3I-2 | V/A = Ohm (W) | E |
| Intensidad de Campo Eléctrico | MLT-3I-1 | N/C | V |
| Capacidad Eléctrica | M-1L-2T4I2 | C/V = Faradio (f) | E |
| Nota: E = escalar y V = vectorial | |||
4.-PROPIEDADES:
1° Principio de Homogeneidad Dimensional o Principio de Fourier (P.H.).
El cual nos indica que cada uno de los términos (monomios) de la ecuación dimensional serán iguales dimensionalmente. (En forma práctica, lo que debemos hacer, es cambiar los signos de SUMA o RESTA por signos de IGUALDAD.
Ejemplo:
En la siguiente ecuación: 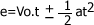 ; luego de aplicar el principio de homogeneidad dimensional nos debe quedar de la siguiente forma:
; luego de aplicar el principio de homogeneidad dimensional nos debe quedar de la siguiente forma: 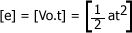
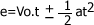 ; luego de aplicar el principio de homogeneidad dimensional nos debe quedar de la siguiente forma:
; luego de aplicar el principio de homogeneidad dimensional nos debe quedar de la siguiente forma: 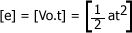
2° Términos Adimensionales:
Los números, los ángulos, los logaritmos, las constantes numéricas (como p) y las funciones trigonométricas, se consideran como términos adimensionales porque no tienen dimensiones, pero para los efectos de calculo, se asume que es la unidad, siempre que vayan como coeficientes, de lo contrario se conserva su valor.
3° No se cumplen la suma y la resta algebraica.
Ejemplo:
[X] + [X] + [X] = [X]
[M] - [M] = [M]
4° Todas las ecuaciones dimensionales deben expresarse como productos y nunca dejarse como cocientes.
Ejemplo:
El término: 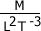 , deberá ser expresado como:
, deberá ser expresado como: 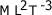
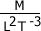 , deberá ser expresado como:
, deberá ser expresado como: 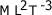











0 comentarios:
Publicar un comentario