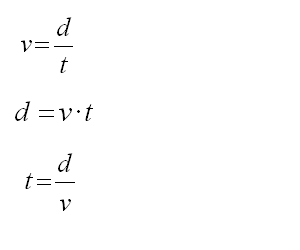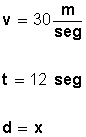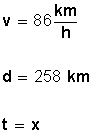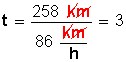MAGNITUDES
1.- DEFINICIÓN: Todo aquello que sea susceptible de aceptar una comparación con otra de su misma especie, es una magnitud (con la consideración de que ésta debe ser inmaterial). Así por ejemplo son magnitudes, la longitud, la masa, el tiempo, el área, el volumen, etc.

2.- CLASIFICACIÓN:
A)Magnitudes fundamentales:
Son todas aquellas que tienen la particular característica de estar presente en todos o casi todos los fenómenos físicos, y además sirven de base para escribir o representar las demás magnitudes.
| SISTEMA INTERNACIONAL DE UNIDADES (S.I.) | ||
| Magnitud | Símbolo | Unidad Básica (Símbolo) |
| Longitud. | L | Metro (m) |
| Masa. | M | Kilogramo (kg) |
| Tiempo. | T | Segundo (s) |
| Intensidad de corriente eléctrica. | I | Ampere o Amperio (A) |
| Intensidad Luminosa. | J | Candela (cd) |
| Temperatura Termodinámica. |
q
| Kelvin (K) |
| Cantidad de Sustancia. | N | Mol (mol) |
| MAGNITUDES AUXILIARES COMPLEMENTARIAS O SUPLEMENTARIAS | |
| Nombre | Unidad Básica (Símbolo) |
| Ángulo Plano. | Radian (rad). |
| Ángulo Sólido. | Estereorradián (sr). |
B)Magnitudes derivadas:
En número es el grupo más grande (ilimitado) en el cada uno puede definirse por una combinación de magnitudes fundamentales y/o auxiliares. Estas combinaciones se consiguen mediante las operaciones de multiplicación, división, potenciación y radicación. Por lo tanto toda magnitud derivada tendrá la siguiente forma: 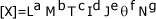 ; donde los exponentes numéricos: a, b, c, d, e, f, g, se conocen como dimensiones.
; donde los exponentes numéricos: a, b, c, d, e, f, g, se conocen como dimensiones.
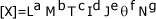 ; donde los exponentes numéricos: a, b, c, d, e, f, g, se conocen como dimensiones.
; donde los exponentes numéricos: a, b, c, d, e, f, g, se conocen como dimensiones.
Ejemplo: área, Volumen, velocidad, aceleración, fuerza, trabajo, energía, calor, etc.
C)Magnitudes escalares:
Son aquellas magnitudes que quedan perfectamente determinadas o bien definidas con sólo conocer su valor numérico o cantidad y su respectiva unidad de medida.
Ejemplo: área, volumen, longitud, tiempo, trabajo, energía, calor, etc.
D)Magnitudes vectoriales:
Son aquellas magnitudes que además de conocer su valor numérico y su unidad, se necesita la dirección y sentido para que dicha magnitud quede perfectamente definida o determinada.
Ejemplo: Velocidad, aceleración, fuerza, gravedad, etc.





 ) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada dimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada
) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada dimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada 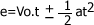 ; luego de aplicar el principio de homogeneidad dimensional nos debe quedar de la siguiente forma:
; luego de aplicar el principio de homogeneidad dimensional nos debe quedar de la siguiente forma: 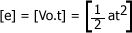
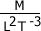 , deberá ser expresado como:
, deberá ser expresado como: 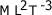
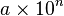
 un número real mayor o igual que 1 y menor que 10, que recibe el nombre de
un número real mayor o igual que 1 y menor que 10, que recibe el nombre de  un número entero, que recibe el nombre de
un número entero, que recibe el nombre de 

![\sqrt[3]{27\cdot 10^{12}} = 3\cdot 10^{4}](http://upload.wikimedia.org/math/a/f/d/afde53997fe13e5e0cceae4f2c01404a.png)
![\sqrt[4]{256\cdot 10^{64}} = 4\cdot 10^{16}](http://upload.wikimedia.org/math/5/e/1/5e1f77893e57922c5712801da277efcf.png)