This is default featured slide 1 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 2 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 3 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 4 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 5 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
martes, 25 de noviembre de 2014
20:09
No comments
ELECTROSTÁTICA
™ Es la parte de la física que se
ocupa de los fenómenos eléctricos generados por las cargas eléctricas en
reposo. La carga eléctrica es la propiedad de la materia responsable de los
fenómenos electrostáticos, cuyos efectos aparecen en forma de atracciones y
repulsiones entre los cuerpos que la poseen.
™ELECTRICIDAD
Y CARGA ELÉCTRICA
™La electricidad es una propiedad
característica de la materia aunque generalmente los cuerpos que nos rodean se
presentan en estado eléctricamente neutro; ello se debe a que la carga positiva
(protones) del núcleo de los átomos es exactamente igual a la carga negativa
(electrones) que se mueven en las cercanías del núcleo.
CUANTIZACION
DE LA CARGA ELÉCTRICA
™La menor cantidad de carga eléctrica posible es la del electrón o
la del proton por esta razón se dice que la carga eléctrica que poseen es la
carga fundamental cuyo valor es 1,6 x〖 10〗^(-19)C.
MEDIOS
DE TRANSMISIÓN ELÉCTRICA
- CONDUCTORES: Son los que permiten que las cargas eléctricas se desplacen con gran facilidad de una región del material a otra.
- AISLANTES: Son los materiales a los que los electrones están fuertemente ligados al núcleo atómico de modo que poseen electrones libres.
MÉTODOS PARA CARGAR ELECTRICAMENTE LA MATERIA
 ™POR FRICCIÓN: Como
ya lo hemos visto, ocurre cuando dos objetos se frotan mutuamente. Este método
es optimo para dos cuerpos aislantes dieléctricos, ya que estos mantienen la
carga eléctrica en las superficies donde fueron frotados.
™POR FRICCIÓN: Como
ya lo hemos visto, ocurre cuando dos objetos se frotan mutuamente. Este método
es optimo para dos cuerpos aislantes dieléctricos, ya que estos mantienen la
carga eléctrica en las superficies donde fueron frotados.
™POR CONTACTO: Este
es un buen método para cargar eléctricamente cuerpos conductores (metales).
™POR INDUCCIÓN: En
este método un cuerpo previamente cargado (inductor) se aproxima aun objeto de
metal; en este se acumulara una cantidad de electrones en un extremo del
cuerpo, cargándose positivamente en el otro extremo.
FUERZAS
ENTRE CARGAS ELÉCTRICAS
- ™ la atracción o repulsión entre las cargas se manifiesta como la fuerza que actúa sobre ellas. Dicha fuerza esta en función de la distancia y el valor de la carga de estas.
- ™ El físico Charles Coulomb, mediante una balanza de torsión estudio las fuerzas con las que se atraían o se repelían los cuerpos cargados y llego a las siguientes conclusiones:
- las fuerzas entre dos partículas cargadas están dirigidas a lo largo de la línea que las une.
- la fuerza que se ejerce entre dos cargas puntuales es atractiva si las cargas son de signos opuestos y repulsiva si las cargas tienen el mismo signo.
lunes, 30 de junio de 2014
21:48
No comments
MOVIMIENTO COMPUESTO
1.- DEFINICIÓN: Es la combinación o superposición de 2 o mas movimientos simples ( M.R.U, M.R.U.V, etc).
2.- PARA ESTUDIAR LOS MOVIMIENTOS COMPUESTOS DEBEMOS:
- Distinguir claramente la naturaleza de cada uno de los movimientos simples componentes.
- Aplicar a cada movimiento componente sus propias ecuaciones.
- Obtener las ecuaciones del movimiento compuesto teniendo en cuenta que:
- La posición de un móvil se obtiene sumando vectorialmente los vectores de posición de los movimientos componentes.

- La velocidad de un móvil se obtiene sumando vectorialmente los vectores velocidad de los movimientos componentes.

- El tiempo empleado en el movimiento compuesto, es igual al tiempo empleado en cada uno de los movimientos componentes.
3.- EJERCICIOS:
Problema n° 1) Se lanza un cuerpo verticalmente hacia abajo con una velocidad inicial de 7 m/s.
a) ¿Cuál será su velocidad luego de haber descendido 3 s?.
b) ¿Qué distancia habrá descendido en esos 3 s?.
c) ¿Cuál será su velocidad después de haber descendido 14 m?.
d) Si el cuerpo se lanzó desde una altura de 200 m, ¿en cuánto tiempo alcanzará el suelo?.
e) ¿Con qué velocidad lo hará?.
Solución del ejercicio n° 1 de Tiro vertical:
Desarrollo:
*Datos:
v0 = 7 m/s
t = 3 s
y = 200 m
h = 14 m
*Ecuaciones:
(1) vf = v0 + g.t
(2) y = v0.t + g.t ²/2
(3) vf ² - v0 ² = 2.g.h
a) De la ecuación (1):
vf = (7 m/s) + (10 m/s ²).(3 s)
vf = 37 m/s
b) De la ecuación (2):
Δh = (7 m/s).(3 s) + (10 m/s ²).(3 s) ²/2
Δ h = 66 m
c) De la ecuación (3):
vf = 18,14 m/s
d) De la ecuación (2):
0 = v0.t + g.t ²/2 - y
*Aplicamos la ecuación cuadrática que dará dos resultados:

t1 = 5,66 s
t2 = -7,06 s (NO ES SOLUCIÓN)
e) De la ecuación (3):
vf = 63,63 m/s
Problema n° 2) Un observador situado a 40 m de altura ve pasar un cuerpo hacia arriba con una cierta velocidad y al cabo de 10 s lo ve pasar hacia abajo, con una velocidad igual en módulo pero de distinto sentido.
a) ¿Cuál fue la velocidad inicial del móvil?.
b) ¿Cuál fue la altura máxima alcanzada?.
Desarrollo:
*Datos:
t = 10 s
y = 40 m
*Ecuaciones:
(1) vf = v0 + g.t
(2) y = v0.t + g.t ²/2
(3) vf ² - v0 ² = 2.g.h
a) Los 10 s se componen de 5 s hasta alcanzar la altura máxima (vf = 0) y 5 s para regresar, de la ecuación (1):
0 = v0 + g.t
v0 = -g.t
v0 = -(-10 m/s ²).(5 s)
v0 = 50 m/s
b) De la ecuación (2):
y = (50 m/s).(5 s) + (1/2).(-10 m/s ²).(5 s) ²
y = 125 m
21:17
No comments
MOVIMIENTO DE CAÍDA LIBRE
1.- DEFINICIÓN: En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo, es frecuente también referirse coloquialmente a éstas como caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general despreciables.

2.-LEYES FUNDAMENTALES DE CAÍDA LIBRE:
a) Todo cuerpo que cae libremente tiene una trayectoria vertical.
b) La caída de los cuerpos es un movimiento uniformemente acelerado.
c) Todos los cuerpos caen con la misma aceleración.
3.- ECUACIONES:

4.-EJEMPLOS:
a) Se deja caer una pelota desde una altura de 20 m. ¿Cuánto tardará en llegar al suelo? ¿Con qué velocidad llega?

b) Desde un avión fue arrojado un cuerpo con una velocidad de 3.5 m/s, calcular el tiempo y la velocidad que alcanzó al caer 0.8 km.
-Primero se calcula la velocidad con la siguiente fórmula.
v2 = v 2i+ 2 gd = (3.5m/s)2 + 2(9.8m/s2)(800m)
v = raí z 15698.25 m2/s2 = 125.29 m/s
-Ahora calculamos el tiempo.
v = vi + gt
t= v-vi / g = 125.29 m/s - 3.5 m/s / 9.8 m/s2= 12.42 s
jueves, 22 de mayo de 2014
21:42
No comments
MAGNITUDES
1.- DEFINICIÓN: Todo aquello que sea susceptible de aceptar una comparación con otra de su misma especie, es una magnitud (con la consideración de que ésta debe ser inmaterial). Así por ejemplo son magnitudes, la longitud, la masa, el tiempo, el área, el volumen, etc.

2.- CLASIFICACIÓN:
A)Magnitudes fundamentales:
Son todas aquellas que tienen la particular característica de estar presente en todos o casi todos los fenómenos físicos, y además sirven de base para escribir o representar las demás magnitudes.
| SISTEMA INTERNACIONAL DE UNIDADES (S.I.) | ||
| Magnitud | Símbolo | Unidad Básica (Símbolo) |
| Longitud. | L | Metro (m) |
| Masa. | M | Kilogramo (kg) |
| Tiempo. | T | Segundo (s) |
| Intensidad de corriente eléctrica. | I | Ampere o Amperio (A) |
| Intensidad Luminosa. | J | Candela (cd) |
| Temperatura Termodinámica. |
q
| Kelvin (K) |
| Cantidad de Sustancia. | N | Mol (mol) |
| MAGNITUDES AUXILIARES COMPLEMENTARIAS O SUPLEMENTARIAS | |
| Nombre | Unidad Básica (Símbolo) |
| Ángulo Plano. | Radian (rad). |
| Ángulo Sólido. | Estereorradián (sr). |
B)Magnitudes derivadas:
En número es el grupo más grande (ilimitado) en el cada uno puede definirse por una combinación de magnitudes fundamentales y/o auxiliares. Estas combinaciones se consiguen mediante las operaciones de multiplicación, división, potenciación y radicación. Por lo tanto toda magnitud derivada tendrá la siguiente forma: 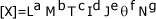 ; donde los exponentes numéricos: a, b, c, d, e, f, g, se conocen como dimensiones.
; donde los exponentes numéricos: a, b, c, d, e, f, g, se conocen como dimensiones.
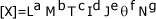 ; donde los exponentes numéricos: a, b, c, d, e, f, g, se conocen como dimensiones.
; donde los exponentes numéricos: a, b, c, d, e, f, g, se conocen como dimensiones.
Ejemplo: área, Volumen, velocidad, aceleración, fuerza, trabajo, energía, calor, etc.
C)Magnitudes escalares:
Son aquellas magnitudes que quedan perfectamente determinadas o bien definidas con sólo conocer su valor numérico o cantidad y su respectiva unidad de medida.
Ejemplo: área, volumen, longitud, tiempo, trabajo, energía, calor, etc.
D)Magnitudes vectoriales:
Son aquellas magnitudes que además de conocer su valor numérico y su unidad, se necesita la dirección y sentido para que dicha magnitud quede perfectamente definida o determinada.
Ejemplo: Velocidad, aceleración, fuerza, gravedad, etc.
21:29
No comments
ANÁLISIS DIMENSIONAL
1.-DEFINICIÓN: Es una herramienta que permite simplificar el estudio de cualquier fenómeno en el que estén involucradas muchas magnitudes físicas en forma de variables independientes. Su resultado fundamental, el teorema de Vaschy-Buckingham (más conocido por teorema  ) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada dimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:
) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada dimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:
 ) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada dimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:
) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada dimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:- Analizar con mayor facilidad el sistema objeto de estudio
- Reducir drásticamente el número de ensayos que debe realizarse para averiguar el comportamiento o respuesta del sistema.
2.-APLICACIONES:
- Detección de errores de cálculo.
- Resolución de problemas cuya solución directa conlleva dificultades matemáticas insalvables.
- Creación y estudio de modelos reducidos.
- Consideraciones sobre la influencia de posibles cambios en los modelos, etc.
| Magnitud Derivada | F.D. | Unidad | Tipo |
| Área o Superficie | L2 | m2 | E |
| Volumen o Capacidad | L3 | m3 | E |
| Velocidad lineal | LT-1 | m/s | V |
| Aceleración lineal | LT-2 | m/s2 | V |
| Aceleración de la Gravedad | LT-2 | m/s2 | V |
| Fuerza, Peso, Tensión, Reacción | MLT-2 | kg . m/s2 = Newton (N) | V |
| Torque o Momento | ML2T-2 | N . m | V |
| Trabajo, Energía, Calor | ML2T-2 | N . m = Joule (J) | E |
| Potencia | ML2T-3 | Joule/s = Watt (W) | E |
| Densidad | ML-3 | kg/m3 | E |
| Peso específico | ML-2T-2 | N/m3 | E |
| Impulso, ímpetu, Impulsión | MLT-1 | N . s | V |
| Cantidad de Movimiento | MLT-1 | kg . m/s | V |
| Presión | ML-1T-2 | N/m2 = Pascal (Pa) | E |
| Periodo | T | s | E |
| Frecuencia Angular | T-1 | s-1 = Hertz (Hz) | E |
| Velocidad Angular | T-1 | rad/s | V |
| Aceleración Angular | T-2 | rad/s2 | V |
| Caudal o Gasto | L3T-1 | m3/s | E |
| Calor Latente específico | L2T-2 | cal/g | E |
| Capacidad Calorífica | ML2T-2q-1 | cal/°K | E |
| Calor Específico | L2T-2q-1 | cal/g.°K | E |
| Carga Eléctrica | IT | A . s = Coulomb (C) | E |
| Potencial Eléctrico | ML2T-3I-1 | J/C = Voltio (V) | E |
| Resistencia Eléctrica | ML2T-3I-2 | V/A = Ohm (W) | E |
| Intensidad de Campo Eléctrico | MLT-3I-1 | N/C | V |
| Capacidad Eléctrica | M-1L-2T4I2 | C/V = Faradio (f) | E |
| Nota: E = escalar y V = vectorial | |||
4.-PROPIEDADES:
1° Principio de Homogeneidad Dimensional o Principio de Fourier (P.H.).
El cual nos indica que cada uno de los términos (monomios) de la ecuación dimensional serán iguales dimensionalmente. (En forma práctica, lo que debemos hacer, es cambiar los signos de SUMA o RESTA por signos de IGUALDAD.
Ejemplo:
En la siguiente ecuación: 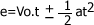 ; luego de aplicar el principio de homogeneidad dimensional nos debe quedar de la siguiente forma:
; luego de aplicar el principio de homogeneidad dimensional nos debe quedar de la siguiente forma: 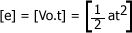
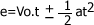 ; luego de aplicar el principio de homogeneidad dimensional nos debe quedar de la siguiente forma:
; luego de aplicar el principio de homogeneidad dimensional nos debe quedar de la siguiente forma: 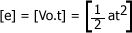
2° Términos Adimensionales:
Los números, los ángulos, los logaritmos, las constantes numéricas (como p) y las funciones trigonométricas, se consideran como términos adimensionales porque no tienen dimensiones, pero para los efectos de calculo, se asume que es la unidad, siempre que vayan como coeficientes, de lo contrario se conserva su valor.
3° No se cumplen la suma y la resta algebraica.
Ejemplo:
[X] + [X] + [X] = [X]
[M] - [M] = [M]
4° Todas las ecuaciones dimensionales deben expresarse como productos y nunca dejarse como cocientes.
Ejemplo:
El término: 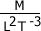 , deberá ser expresado como:
, deberá ser expresado como: 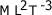
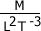 , deberá ser expresado como:
, deberá ser expresado como: 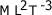
20:49
No comments
LA NOTACIÓN CIENTÍFICA
1.-DEFINICIÓN: La notación científica (o notación índice estándar) es una manera rápida de representar un número utilizando potencias de base diez. Esta notación se utiliza para poder expresar muy fácilmente números muy grandes o muy pequeños.
Los números se escriben como un producto:
siendo:
 un número real mayor o igual que 1 y menor que 10, que recibe el nombre de coeficiente.
un número real mayor o igual que 1 y menor que 10, que recibe el nombre de coeficiente. un número entero, que recibe el nombre de exponente u orden de magnitud.
un número entero, que recibe el nombre de exponente u orden de magnitud.
La notación científica utiliza un sistema llamado coma flotante, o de punto flotante en países de habla inglesa y en algunos hispanohablantes.
2.-ESCRITURA:
- 100 = 1
- 101 = 10
- 102 = 100
- 103 = 1 000
- 104 = 10 000
- 105 = 100 000
- 106 = 1 000 000
- 107 = 10 000 000
- 108 = 100 000 000
- 109 = 1 000 000 000
- 1010 = 10 000 000 000
- 1020 = 100 000 000 000 000 000 000
- 1030 = 1 000 000 000 000 000 000 000 000 000 000
10 elevado a una potencia entera negativa –n es igual a 1/10n o, equivalentemente 0, (n–1 ceros) 1:
- 10–1 = 1/10 = 0,1
- 10–2 = 1/100 = 0,01
- 10–3 = 1/1 000 = 0,001
- 10–9 = 1/1 000 000 000 = 0,000 000 001
- 10-12 = 1/1 000 000 000 000 = 0,000 000 000 001
- 10-15 = 1/1 000 000 000 000 000 = 0,000 000 000 000 001
- 10-17 = 1/ 1 000 000 000 000 000 00 = 0,000 000 000 000 000 01
Por tanto, un número como: 156 234 000 000 000 000 000 000 000 000 puede ser escrito como 1,56234×1029

3.-OPERACIONES:
A)Suma:
Siempre que las potencias de 10 sean las mismas, se deben sumar los coeficientes, dejando la potencia de 10 con el mismo grado. En caso de que no tengan el mismo exponente, debe convertirse el coeficiente, multiplicándolo o dividiéndolo por 10 tantas veces como se necesite para obtener el mismo exponente.
Ejemplos:
- 2×105 + 3×105 = 5×105
- 3×105 - 0.2×105 = 2.8×105
- 2×104 + 3 ×105 - 6 ×103 = (tomamos el exponente 5 como referencia)
- = 0,2 × 105 + 3 × 105 - 0,06 ×105 = 3,14 ×105
B)Multiplicación:
Para multiplicar cantidades escritas en notación científica se multiplican los coeficientes y se suman los exponentes.
Ejemplo:
- (4×1012)×(2×105) =8×1017
C)División:
Para dividir cantidades escritas en notación científica se dividen los coeficientes y se restan los exponentes.
Ejemplo: (48×10-10)/(12×10-1) = 4×10-9
D)Potenciación:
Se eleva el coeficiente a la potencia y se multiplican los exponentes.
Ejemplo: (3×106)2 = 9 ×1012.
E)Radicación:
Se debe extraer la raíz del coeficiente y se divide el exponente entre el índice de la raíz.
Ejemplos:
19:24
No comments
MOVIMIENTO RECTILÍNEO UNIFORME VARIADO ( MRUV)
1.-DEFINICIÓN: Es el de un móvil cuya aceleración (a) permanece constante en modulo y dirección
2.-CARACTERÍSTICAS:
· La velocidad es directamente proporcional al tiempo
· La rapidez varia y según esta aumente o disminuya, el movimiento es acelerado o retardado, respectivamente.
· La rapidez varia y según esta aumente o disminuya, el movimiento es acelerado o retardado, respectivamente.
Un cuerpo posee movimiento rectilíneo uniformemente variado cuando cumple las siguientes condiciones:
A) La trayectoria que recorre es una línea recta.
B) La velocidad cambia, permaneciendo constante
3.- FORMULAS:
Usar : (+); si el movimiento es acelerado.
Usar : (-); si el movimiento es retardado.
Vo = velocidad inicial
Vf = velocidad final a = aceleración
t = tiempo
e = espacio o distancia
t = tiempo
e = espacio o distancia
4.- UNIDADES EN EL S.I:
|
V0
|
Vf
|
e
|
t
|
a
|
|
m/s
|
m/s
|
m
|
s
|
m/s2
|
5.- EJERCICIOS:
A) Calcula la distancia recorrida por un móvil que parte de reposo y alcanza una velocidad de 52 Km/h en 5 segundos.
Usaremos la formula:
D = Vi . T +/- ½ . a . T2
Tenemos como datos la velocidad final y el tiempo. Como el móvil parte del reposo su velocidad inicial es 0, por lo tanto el primer termino se anula.
D = + ½ . a . T2
El signo de la aceleración queda positivo ya que la velocidad aumenta de 0 al valor final de 52 Km/h.
La aceleración no la tenemos pero la podemos calcular. Para esto será conveniente previamente pasar la unidad de velocidad de Km/h a mts/seg para que sea compatible con el tiempo que est expresado en segundos.
Ahora procedemos a calcular la aceleración:
D = + ½ . 2,89 mts/seg2 . (5 seg)2
D = 36.125 mts.
B) Calcula la velocidad final de un móvil que viajando a una velocidad de 22 mts/seg acelera a razón de 2 mts/seg2 en 4 seg.
De la formula de aceleración hay que despejar la velocidad final.
a = (Vf – Vi) / T
Vf = a x T + Vi
Vf = 2 mts/seg2 x 4 seg + 22 mts/seg
Vf = 30 mts/seg
Suscribirse a:
Entradas (Atom)













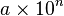

![\sqrt[3]{27\cdot 10^{12}} = 3\cdot 10^{4}](http://upload.wikimedia.org/math/a/f/d/afde53997fe13e5e0cceae4f2c01404a.png)
![\sqrt[4]{256\cdot 10^{64}} = 4\cdot 10^{16}](http://upload.wikimedia.org/math/5/e/1/5e1f77893e57922c5712801da277efcf.png)











